Die Transformationskurve zeigt die Produktionsmöglichkeitengrenze einer Volkswirtschaft.

Mit dem Begriff Produktionsmöglichkeitengrenze, den man als Synonym für Transformationskurve verwenden kann, ist sie schon recht gut beschrieben, denn sie zeigt, was eine Volkswirtschaft maximal herstellen kann. Für eine reale Volkswirtschaft mit hunderttausenden von Gütern ist sie nicht konstruierbar. Sie ist vielmehr ein theoretisches Konzept und zunächst vor allem bei der Klärung einiger grundlegender Begriffe und Sachverhalte von Nutzen.

Zur Vorstellung der Transformationskurve treffen wir einige Annahmen. Sie sind zwar vollkommen realitätsfern, erleichtern uns jedoch das Verständnis ungemein:

1. Es gibt nur einen einzigen, homogenen Produktionsfaktor.
2. Der Produktionsfaktor ist immer vollbeschäftigt.
3. Es gibt nur zwei Endprodukte.
4. Die Technik ist gegeben.
5. Alles ist eindeutig vorherbestimmt (es gibt keine Zufälle).

Bei dem Produktionsfaktor soll es sich um Arbeit handeln. Die Menge an Arbeit messen wir mit dem Symbol $L$ ("labour"). Ein $L$ soll der standardisierten Leistung von einer Arbeitskraft je Tag entsprechen. Wir nehmen an, in der betrachteten Periode stehen 100 Einheiten $L$ zur Verfügung.

Die beiden Endprodukte (Güter) nennen wir $X$ und $Y$. Mit diesen Symbolen werden zugleich ihre Mengen angegeben.

Wir sind in der Lage, die Prozesse, wie aus Arbeit die beiden Güter $ $und $Y$ entstehen, zu beschreiben. Dazu verwenden wir Produktionsfunktionen. Sie geben an, welche Menge an Gütern (Output) maximal erzeugt werden kann, wenn eine bestimmte Menge an Produktionsfaktoren eingesetzt (Inputs) wird.

Für das Gut X soll folgende Produktionsfunktion gelten:

$$X=2 \times L_X \tag{1} $$

Die Arbeitsmenge $L$ ist mit $X$ indiziert, um zu verdeutlichen, dass es sich um die in der Produktion von $X$ eingesetzte Arbeitsmenge handelt. Für jede vorgegebene Menge an Arbeit $L_X$ wissen wir nun, wie viele $X$ in der Betrachtungsperiode hergestellt werden. Wenn wir zum Beispiel für $L_X$ den Wert 20 annehmen, werden 40 $X$ hergestellt. Offensichtlich verdoppelt sich mit dem Faktoreinsatz $L_X$ die Produktionsmenge $X$. Die Produktionsfunktion ist also linear. Man sagt auch: Die Technik ist linear. Daneben gibt es noch weitere Formulierungen, die denselben Sachverhalt zum Ausdruck bringen: Die Produktionselastizität des Faktors Arbeit hinsichtlich des Outputs $X$ ist gleich eins. Die Skalenerträge sind konstant. Das soll uns hier aber nicht weiter interessieren.

Für das zweite Gut $Y$ wählen wir eine etwas kompliziertere Technologie:

$$Y=10 \times \sqrt{L_Y} \tag{2} $$

Würden zum Beispiel 49 Faktoreinheiten $L_Y$ in der Y-Produktion eingesetzt, dann ergäbe sich eine Produktion von 70 $Y$. Da die Technologie etwas komplizierter ist, verschaffen wir uns mit Hilfe einer Tabelle und eines Diagramms einen besseren Überblick. Um dabei ohne Taschenrechner auszukommen, betrachten wir nur Quadratzahlen als Einsatzmengen von $L_Y$.

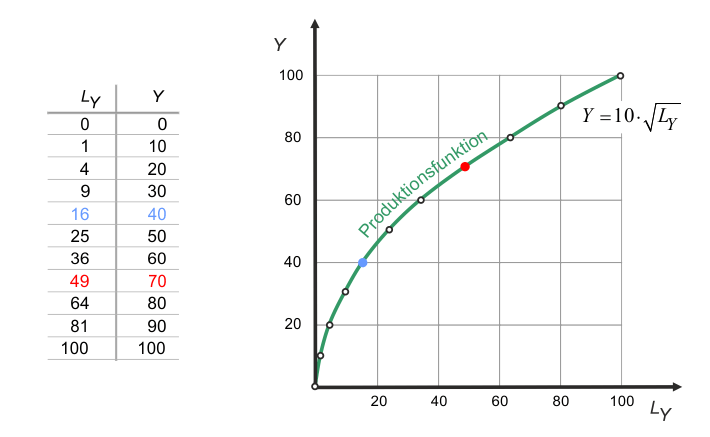
Zwei Wertepaare sind farblich hervorgehoben, damit deutlich wird, wie sie in das Diagramm in Abb. 1 übertragen werden.

Insgesamt stehen 100 Einheiten Arbeit zur Verfügung, die entweder in der Produktion von $X$ oder in der Produktion von $Y$ eingesetzt werden können. Da wir von Vollbeschäftigung ausgehen, gilt:

$$L_X + L_Y = 100 \tag{3}$$

Diese Gleichung wird Vollbeschäftigungsbedingung genannt.

Analytisch ist es nun ein einfaches Unterfangen, die Produktionsmöglichkeiten zu berechnen. Dazu werden die Produktionsfunktionen (1) und (2) nach den Arbeitsmengen aufgelöst und in die Vollbeschäftigungsbedingung  (3) eingesetzt:

$$L_X = 0,5X \tag{4}$$ $$L_Y = \frac{Y^2}{100} \tag{5}$$ $$0,5X + 100Y^2 = 100 \tag{6}$$ $$ X=200- \frac{Y^2}{50} \tag{7}$$

Für jeden Wert von $Y$ können wir jetzt mittels (7) berechnen, wie viele $ $bei Vollbeschäftigung hergestellt werden können. Wir stellen eine Tabelle mit 10er Schritten auf, um genügend Stützpunkte zu gewinnen und die Transformationskurve grafisch abbilden zu können:

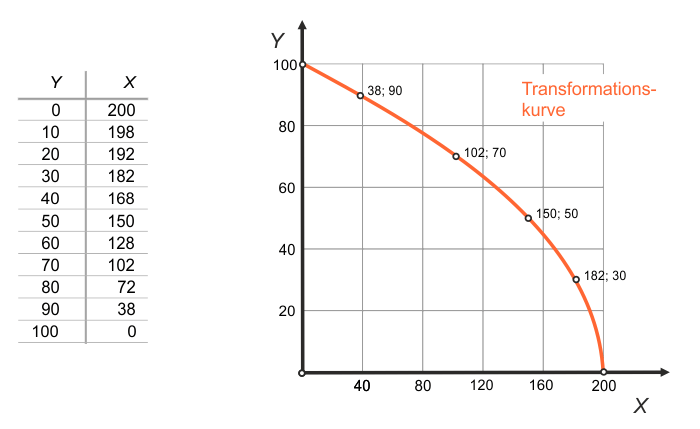
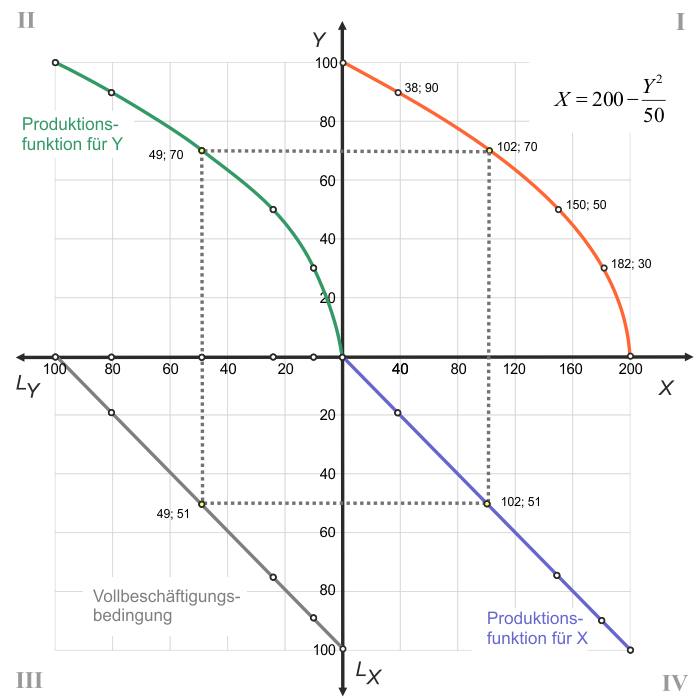
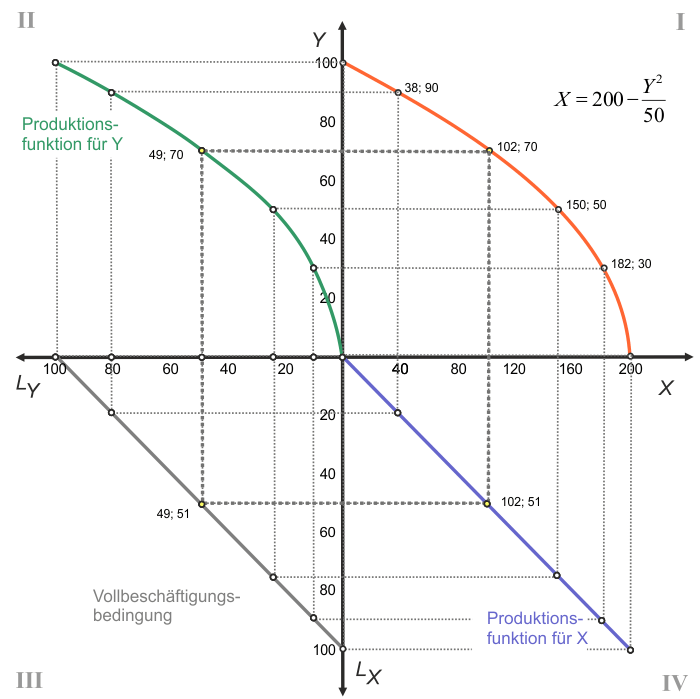
Alternativ ist eine vollständige grafische Konstruktion der Transformationskurve möglich. Dazu wird in Abb. 3 ein Vierfelderdiagramm aufgespannt. In den Quadranten II und IV sind die beiden Produktionsfunktionen eingezeichnet. Quadrant II zeigt die bereits betrachtete Produktionsfunktion für $Y$. Im Unterschied zu Abb. 1 ist hier die $L_Y$-Achse von rechts nach links zu lesen.

Die Gerade im Quadrant III sorgt für die Einhaltung der Vollbeschäftigungsbedingung. Egal, wo wir uns auf der Geraden befinden, die Summe der Beschäftigung in den beiden Produktionen von $X$ und $Y$ ist immer gleich 100. Ausgehend von einer Beschäftigung von 49 Einheiten $L$ in der $Y$-Produktion und 51 Einheiten $L$ in der $X$-Produktion lässt sich der Punkt $(X; Y)=(102; 70)$ konstruieren. Wird diese Vorgehensweise mit ausreichend vielen Punkten wiederholt, lässt sich die Transformationskurve einzeichnen (s. klickbares Diagramm).

Mit einem Blick auf die Bestandteile des Vierfelderdiagramms

1. Vollbeschäftigung einer gegebenen Menge an Faktoren (Quadrant III)
2. Bekannte Technologie (Quadranten II und IV)

lässt sich nun etwas präziser als zu Beginn dieses Beitrags definieren:

Denn ganz offensichtlich ergäbe sich eine andere Grenze der Produktionsmöglichkeiten, wenn sich eine oder beide Produktionsfunktionen änderten oder der Faktorbestand zu- oder abnähme.